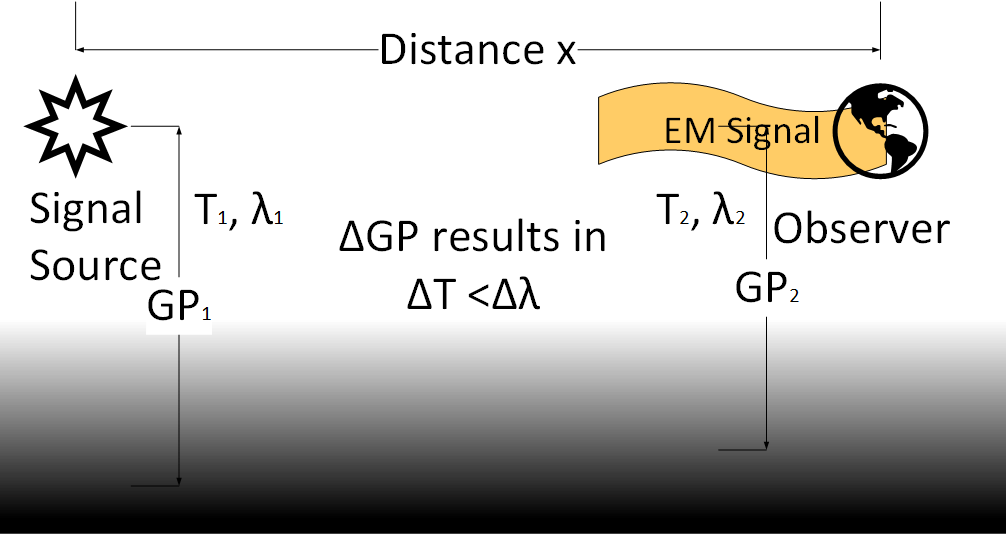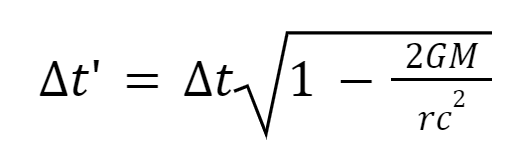
Gravitational time dilation.
This impacts the perceived wavelength of a received signal if the potential is different than the source.
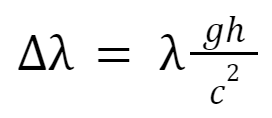
Change of wavelength due to GP
This impacts the observed wavelength if there is a GP differential.
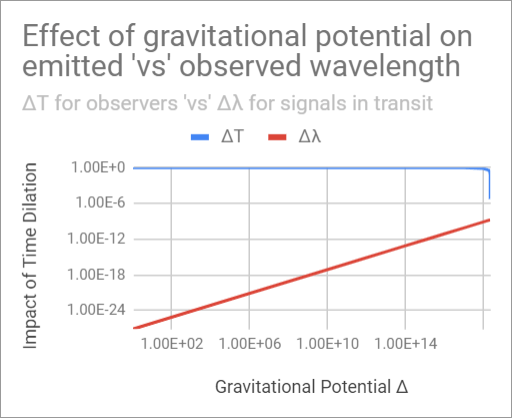
Linear result 'vs' Logarithmic
Where the impact of time dilation is negligible to the source and observer (except for the most dilated conditions), the impact to in-transit wavelengths is linearly proportional.